Градиентный спуск

Градиент

По определению функция зависит от одной или нескольких величин. При изменении этих величин функция может увеличиваться, уменьшаться или оставаться на месте. Градиент же определяет направление максимального увеличения этой функции и его крутизну. Градиент со знаком минус называется антиградиентом и определяет максимальный спуск.

Чем больше стрелка на картинке тем больше положительный наклон функции, а значит и его значение.

Математически же градиент определяется как вектор, составленный из частных производных.

Если же объяснять очень простым языком, то можно представить, что мы стоим на вершине холма и хотим максимально быстро спуститься с него. Поэтому мы будем выбирать направление где крутизна спуска больше всего.

Градиентный спуск

Используя градиент можно определять в какой стороне у функции минимум, поэтому на его основе придумали метод нахождения локального экстремума. Для нахождения минимума направление задаётся антиградиентом.

Если сравнивать с примером из предыдущего пункта поменялось лишь количество переменных. Вместо производной функции от 1 переменной, теперь собирается вся информация по производным всех переменных в вектор, который называется градиентом. И вдоль антиградиента с каким-то маленьким шагом $\alpha$ (определяющий скорость обучения) можно будет найти минимум функции.

Продолжение линейной регрессии

Напомню, что наша функция ошибка была такой: $MSE=\frac{\sum_{i=1}^n (\hat{y_i}-y_i)^2}{n}$ А зависит она только от двух коэффициентов модели $w,b$ : $y = wx+b$ Получается, что для градиентного спуска нам надо посчитать две частных производных по $w$ и $b$ . $der_w=\frac{\sum_{i=1}^n (\hat{y_i}-y_i)(x_i)}{n}$$der_b=\frac{\sum_{i=1}^n (\hat{y_i}-y_i)}{n}$ Теперь зная частные производные по всем аргументам функции, мы можем применить метод градиентного спуска.

Для наглядности можно начать с $w=-1$ , $b=0$ . И ограничивающим параметром альфа равным 0.05.

На каждой итерации видно как модель уменьшает свою среднеквадратичную ошибку.

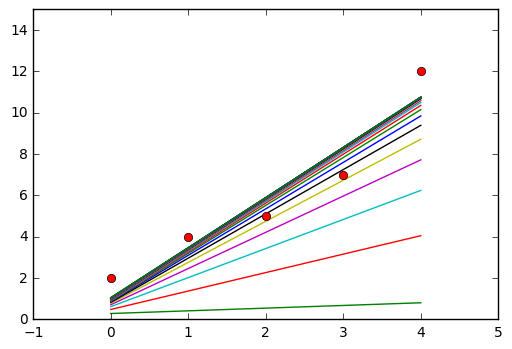
За эпоху считается проход по всей обучающей выборке

В результате за 30 итераций (эпох) мы получили следующие результаты:

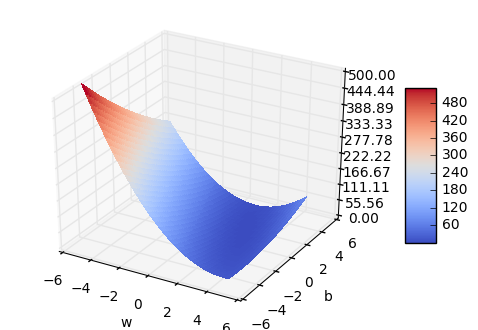
Ошибка уменьшилась с 80 до 1. Для наглядности я вывел график зависимости ошибки от параметров $w,b$ . В нем не очень хорошо видно минимум, но можно оценить его примерное расположение.

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter

x, y = np.array([0,1,2,3,4]), np.array([2,4,5,7,12])
w, b = -1, 0
alpha = 0.05

f = lambda x: x*w+b
MSE = lambda x,y: np.sum((f(x)-y)**2)/5 
w_der = lambda x,y: np.sum((f(x)-y)*x)/5
b_der = lambda x,y: np.sum((f(x)-y))/5

for i in range(30):
    print (w,b, MSE(x,y))
    plt.plot(x, f(x))
    w = w - alpha*w_der(x,y)
    b = b - alpha*b_der(x,y)


plt.plot(x, y, 'ro')
plt.axis([-1, 5, 0, 15])
plt.show()

fig = plt.figure()
ax = fig.gca(projection='3d')
w = np.arange(-5, 5, 0.25)
b = np.arange(-5, 5, 0.25)
W, B = np.meshgrid(w, b)

MSE_test = lambda x,y,w,b: np.sum((x*w+b-y)**2)/5
zs = np.array([MSE_test(x,y,wp,bp) for wp, bp in zip(np.ravel(W), np.ravel(B))])
Z = zs.reshape(W.shape)
print (W.shape, B.shape, Z.shape)

surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm,
                       linewidth=0, antialiased=False)
ax.set_zlim(0, 500)

ax.zaxis.set_major_locator(LinearLocator(10))
ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f'))
ax.set_xlabel('w')
ax.set_ylabel('b')
fig.colorbar(surf, shrink=0.5, aspect=5)

plt.show()