Линейная регрессия
Линейная регрессия является самым простым для понимая примером алгоритма машинного обучения.
Данный метод относится к обучению с учителем. В качестве выходного значения должен выдать некоторое число, зависящее от входного значения. Таким образом строится зависимость между двумя переменными (для данного одномерного случая), которую можно использовать для дальнейших предсказаний.
Допустим мы хотим предсказывать значения , зависимые от .
Обучающая выборка:
| x | y |
|---|---|
| 0 | 2 |
| 1 | 4 |
| 2 | 5 |
| 3 | 7 |
| 4 | 12 |
Модель линейной регрессии представлена в виде: Вместе и называются параметрами/коэффициентами модели.
Как видно из уравнения модели, мы хотим построить прямую, которая максимально будет описывать наши данные. Имея задачу и набор данных осталось определить меру качества нашей модели. В качестве такой меры удобно использовать среднеквадратичную ошибку (mean squared error). Допустим и . Теперь можно построить график нашей модели (линии) относительно наших переменных (x, y):

В данном случае ошибка равна . Внутреняя чуйка подсказывает, что скорее всего это не самое лучшее решение. Поэтому надо обучать модель так, чтобы эта ошибка была минимально возможной.
Если немного отвлечься от нашей функции ошибки, которая зависит от 2 переменных, то хорошо бы поэкспериментировать с функцией от 1 переменной и понять, каким способом можно искать минимум.
Пусть есть функция: И мы находимся сейчас в точке .

Имея лишь информацию о собственном нахождении и самой функции надо найти минимум. Конечно можно случайно менять и смотреть увеличивается ли наша функция. Но есть способ получше.
По определению наклон функции описывается его производной и если мы можем её посчитать (числовым или аналитическим способом), то двигаясь в сторону уменьшения функции можно достичь минимума (локального или глобального) или седловой точки. Только не стоит забывать, что производные могут быть огромными и поэтому нужно ограничивать шаг неким параметром . Это очень важный параметр, потому что от него зависит скорость поиска минимума и его точность. Возьмем и посмотрим на наш путь по функции.

Сразу видно, что мы достигли минимума или по-крайней мере очень близки к нему.
Но если взять , то за такое же количество итераций (50) мы очень медленно приближаемся в сторону минимума.
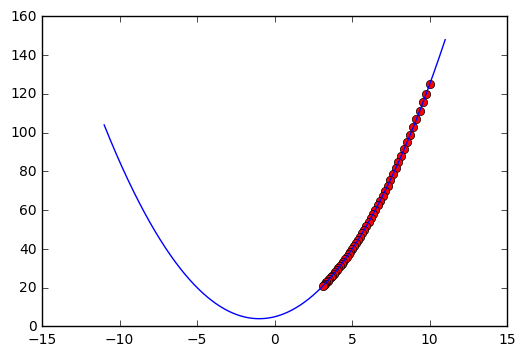
А вот здесь :

Тут мы практически всего за несколько итераций достигли минимума, но вот только первым же шагом мы его перепрыгнули, потом опять и опять. Это может быть опасно при работе со сложными функциями, но есть и шанс что он будет вообще расходиться в бесконечность. Поэтому нужно тщательно выбирать максимально маленький параметр для определенной задачи. На практике можно просто менять его в разумных пределах и выявлять лучший.
Код:
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
x1 = np.linspace(-11,11,1000)
y = lambda x: x**2+2*x+5
der = lambda x: 2*x+2 # производная
x=10
for i in range(50):
plt.plot(x, y(x), 'ro')
x = x - 0.6*der(x) # 0.6 - это и есть параметр альфа
print (x)
plt.plot(x1,y(x1))
plt.show()
Вернемся к нашей функции ошибки. Она зависит от двух переменных в отличие от примера выше, но это не может помешать нам одновременно идти в направление уменьшения ошибки по каждой переменной. Данный метод называется градиентным спуском и описан в следующем пункте.